B Plus Tree Index

B+ Tree

Self-balancing
Ordered
searches, sequential access, insertion and deletion in O(log n)

Properties

Perfectly balanced (every leaf node is at the same depth in the tree)
Every non-root node has key count of (M / 2 - 1) <= #keys <= (M - 1)
Every inner node with k keys has k + 1 non-null children

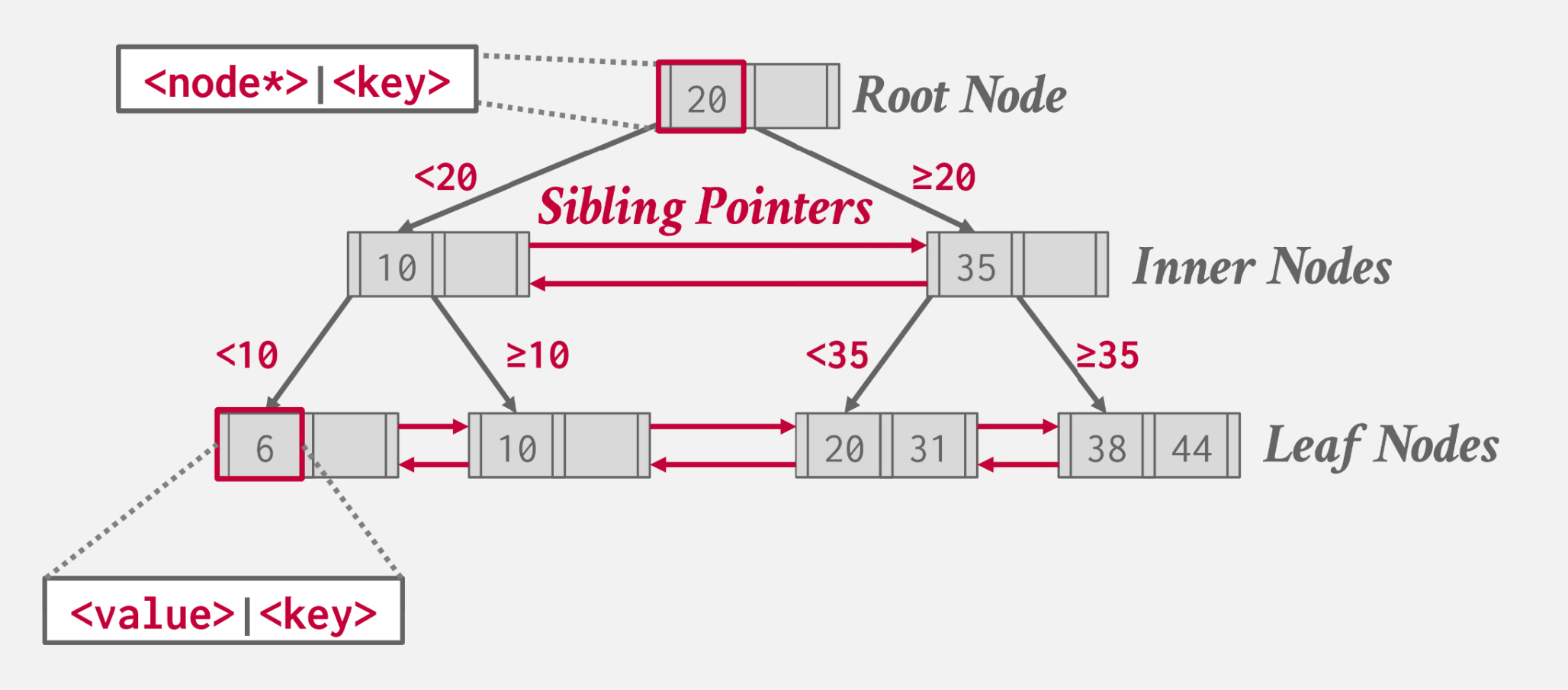
B Tree VS. B+ Tree

B 树在树的任意节点存储键值对，而 B+ 树只在叶子节点存储值。

B+ 树具有更好的并发访问性能和顺序 I/O 性能

Basic Operations

B+ 树操作可视化，仅供参考 B+ Trees

Insert

通过大小关系找到目标叶子节点 L，插入 entry

如果插入节点后的元素数小于 M，结束

如果插入节点后的元素数等于 M，分割节点，将 key 提升到父节点

Delete

通过大小关系找到目标叶子节点 L，删除 entry

如果删除节点后的元素数量大于 M / 2 - 1，结束

如果删除节点后的元素数量等于 M / 2 - 1，则进行重新分配，从相邻的兄弟叶子节点分配 entry。

如果重新分配失败，即节点和兄弟节点在删除节点后元素数都小于等于 M / 2 - 1，则合并两个叶子节点

Selection Conditions

Duplicate Keys

对于插入以及存在的 key，有两种方法：

和插入不同的 key 一样直接插入
添加 overflow 节点，将 key 插入 overflow 节点

Clustered Indexes

将表按照主键的顺序存储在硬盘上

Index Scan Page Sorting

找到查询需要的所有 tuple，基于其 page ID 进行排序

B+ Tree Design Choices

Node Size

The slower the storage device, the larger the optimal node size for a B+Tree.

HDD: ~1MB
SSD: ~10KB
In-Memory: ~512B

Merge Threshold

使用一个节点合并阈值以延迟合并操作

Delaying a merge operation may reduce the amount of reorganization.

It may also be better to just let smaller nodes exist and then periodically rebuild entire tree.

Variable-Length Keys

Pointers

在节点中存储指向 key 实际数据的指针
会导致产生非连续 IO (nonsequential IO)

Variable-Length Nodes

每个节点的长度可变
需要谨慎的内存管理

Padding

总是将键拓展到键类型的最大长度

Key Map / Indirection

将键值对另外存储，在 B 树中只存储键值对的指针

Intra-Node Search

Linear: 直接进行线性查找

使用 SIMD 进行批量比较

Binary: 进行二分查找
Interpolation

Optimizations

Prefix Compression(,前缀压缩,)

robbed	robbing	robot

Prefix: rob#

bed	bing	ot

Deduplication

K1	V1	K1	V2	K1	V3	K2	V4

K1	V1	V2	V3	K2	V4

Suffix Truncation

有时不需要存储完整的键，可以将其截断进行存储

Pointer Swizzling

一般在访问某个特定 page 时，会使用逻辑指针 pageid 在对应 table 中查询进行访问，对于已经被固定在内存中的 page 可以直接通过物理指针进行访问以减少内存 I/O，提升访问性能。

Bulk Insert

通过先排序键再从下到上建立索引，快速为现有的表构建新的 B+ 树

在一些时候，对 B+ 树的插入和删除操作会造成很大的开销。

Write-Optimized B+ Tree Bε-trees

当进行写入时，不立即应用更新，而是将操作存储到 inner nodes 的日志缓冲区（或 mod(,modify,) log）

当缓冲区已满时，将日志中的条目按照更新的键传递到子节点；若无子节点，则应用更新。

点此查看原文